Delta: Assessing Probabilities Based on the Break-even price

As we saw in an earlier article, delta measures how much an option’s price moves in relation to a change in the price of the underlying asset. Delta is a variable from the Black-Scholes option pricing model, and it is also used in the industry as an approximation of the probability that the option will be in-the-money at expiration.* So we say that a deep in-the-money option, i.e. an option with a delta of close to 1, has an almost 100% chance of being in-the-money at expiration. A deep out-of-the-money option, with a delta close to 0, will therefore have an almost 0% chance of being in-the-money at expiration. And an at-the-money option, with a delta close to 0.5, will have a close to 50% chance of being in-the-money at expiration.
Now consider the following example, taken from the Montréal Exchange’s Options Calculator.

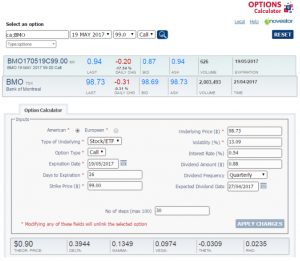
As we can see, the call options BMO 170519 C 99.00 have a theoretical value of $0.90 and a delta of 0.3944. We can say that the probability that this call option will be in-the-money at expiration is approximately 39.44%, and it will be worth at least $0.01. But if I have paid $0.90 for the option and it is only $0.01 in-the-money, I will incur a loss of $0.89 on my option. What I would like to know, at the time that I buy my call option, is the probability that it will turn a profit at expiration, i.e. that it will be worth more than my break-even price of $99.90 (the $99 strike price plus the $0.90 premium).
To find this probability, all we need to do is find the delta of a call option with a strike price of $99.90. This particular strike price is not available among the strike prices listed on the Montréal Exchange, so we will interpolate an answer based on the closest strike price, which is $100.

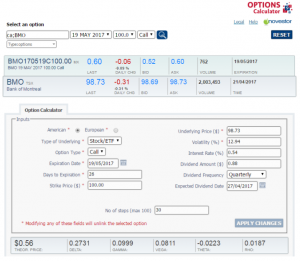
As we can see, the call option BMO 170519 C 100.00 has a delta of 0.2731, for a 27.31% probability of being in-the-money at expiration. Based on the available data, we can find the approximate delta of a theoretical call option with a strike price of $99.90 — our break-even price — as follows. Note that since the specific strike price of $99.90 does not exist (it is not traded on the markets), this exercise only allows us to estimate the probability of our strategy succeeding.

Distance between the benchmark strike prices: $1 ($100 – $99)
Difference between the deltas: -0.1213 (0.2731 – 0.3944)
Difference between the break-even price and the lower strike price: $0.90 ($99.90 – $99.00)
This difference represents 90% of the distance between the benchmark strike prices ($0.90/$1.00)
The delta we are looking for is obtained as follows:
[(4) 90% x (2) -0.1213] + [delta of the lower strike price] 0.3944 = -0.10917 + 0.3944 = 0.2852

Consequently, we can say that by buying the call options BMO 170519 C 99.00 at $0.90, our chances of realizing a profit are approximately 28.52%. We know that there is a 39.44% probability that the price of BMO will be greater than $99. We can therefore say that there is a 60.56% probability (1 – 0.3944) that the price of BMO will be below $99. This means that there is a 60.56% chance that we will incur a total loss. So we now have several important pieces of information for determining whether our chances of success are good enough, and whether our objectives for the underlying asset are realistic in the long term. This is a procedure that can be used to approximate the probability of realizing profits in all our strategies, from the simplest spreads to the most complex.

Good luck with your trading, and have a good week!

* Even though delta is used as a good approximation of the probability that the option will be in-the-money at expiration, there is another variable that provides us with this probability, and with greater precision. We use delta because it is easy to obtain from the most frequently used options software applications.
Black-Scholes formula for a stock option1 c = S0 * N(d1) – VA(K) * N(d2)
1 American or European-style stock option on stocks that do not pay dividends prior to the expiry date of the option.
Where:
c = Value of the stock option
S0 = Current price of the underlying asset
VA(K) = Current value of the strike price
N(d1) and N(d2) are functions of standard normal distribution giving the probability that a normally distributed variable will be less than d1 and d2.
N(d1) represents delta, and N(d2) represents the probability that the option will be in-the-money at expiration. Generally speaking, an option’s delta will be higher than the probability of it being in-the-money, and this spread becomes wider with a longer time to expiration and with higher volatility in the price of the underlying asset.

The strategies presented in this blog are for information and training purposes only, and should not be interpreted as recommendations to buy or sell any security. As always, you should ensure that you are comfortable with the proposed scenarios and ready to assume all the risks before implementing an option strategy.