Call Put Parity: How to Transform Your Positions

I have been told frequently – and surely so have you – that selling cash-secured puts is a very risky strategy. Haven’t you? The main reason put forward for not using this strategy is that you could be forced to buy the security, even if the company had just gone bankrupt. In this light, the strategy rightly raises fears. Who would want to buy a security at a high price when it no longer has any value? Because that is exactly what selling cash-secured puts forces you to do: be obliged to buy the underlying asset if holders exercise their right to sell it.

At the option’s expiry date, if the security is trading at a price that is below the strike, holders will exercise their right to sell the shares, and you will be forced to buy those shares at a loss. The risk of incurring a loss is therefore very real. But what about selling covered calls? To this question, the most frequent reply is that this strategy is perfectly fine, since it can generate additional income through the sale of call options, and offers quite substantial protection against a potential drop in the stock price. And this viewpoint is not wrong! What about the company’s bankruptcy risk? A frequent reply is that this risk is very low and that the same can be said of all securities. And once again, this argument is not wrong. But why is the bankruptcy risk given more weight when selling cash-secured puts than it is when selling covered calls? Undoubtedly, perceptions play a role here, since in reality, these two strategies are identical across the board, as you can see in the following charts.

Selling Covered Calls

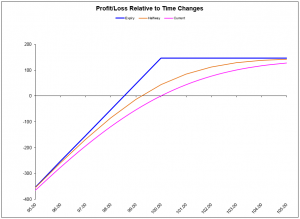
Selling covered call options:

Holding 100 XYZ at $100 and selling one XYZ 100 call option at $1.50

Selling Cash-Secured Puts

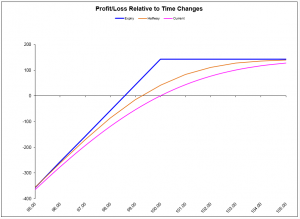
Selling cash-secured put options:

Selling one XYZ 100 put option at $1.50

In fact, the two strategies have the same profit and loss diagram, so they carry the same potential risk and profit. These two graphs offer a proof that selling cash-secured puts is no riskier than selling covered calls. Case settled.

What we have just seen is that one position can be transformed into another. This means that when we have shares in our portfolio, we can transform them by adding an option position. In the case discussed above, we transformed our share position into the sale of cash-secured puts by selling a call option. This is due to a basic principle in option valuation: call put parity. Under the call put parity principle, a call option can be transformed into a put option, and vice-versa.*

Let us consider the following case. Instead of selling a call option, we add the purchase of a put option. Our position will then be equivalent to holding a call option. In fact, the profit potential remains, but the loss in the event of a drop in price is now limited due to the purchase of put options. This means that the profit and loss diagram is the same as if we held a call option as illustrated in the following graphs.

Holding the Security and Purchasing a Put Option

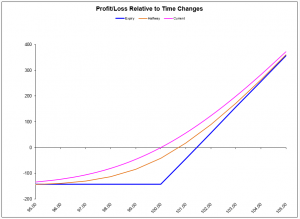
Holding the security and purchasing a put option:

Holding 100 XYZ at $100 and purchasing one XYZ 100 put option at $1.50

Purchasing a Call Option

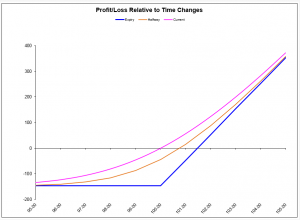
Purchasing a call option:

Purchasing one XYZ 100 call option at $1.50

As you can see, the two positions have the same profit and loss diagram, which features unlimited potential for profit if the stock rises and a limited loss if it falls. We have seen two ways to transform one position into another and they are far from being the only ones. In fact, there is an abundance of different permutations that allow us to transform one position into another. All you need to do is apply a bit of algebra, using the following call put parity formula:

Call put parity formula

c + PV(K) = p + S

where

• c = call
• PV(K) = Present value of the strike
• p = put
• S = Value of the underlying asset

To simplify the calculations, we omit the variable PV(K). The formula then becomes:

c = p + S

As seen above, a call option is equal to holding the security (S) and a put option (p).

Now let us try a few variations.

p = c – S

This shows that a put option can be obtained by purchasing a call option (c) and selling the security short (- S).

-p = -c + S

In this case, as we have seen above, selling a put option (-p) can be transformed into selling a call option (-c) and holding the security (S).

-c = -p – S

Selling a call option (-c) may be replicated by selling a put option (-p) and selling the security short (-S).

Various other permutations of the formula are possible, and feel free to try them all on your own. This is the principle that keeps the options market in equilibrium. So if the call options on a particular strike and expiry date were to increase sharply, it would be possible to buy both the corresponding put options and the shares, and to sell the call options in response to the demand. These are called “arbitrage transactions” that aim to keep all the options in a given class of options within a price range taking into account supply and demand.

*Note that for the purposes of this article, we have discussed call put parity based on European options, i.e. options that can be exercised only at their expiry date. For European options, call put parity works perfectly. For American options, i.e. options that can be exercised before their expiry date, this relationship is imperfect, since the call option can be exercised before the put option, and vice-versa. This means that American call and put options may have different effective expiry dates, rendering the call put parity principle inoperative. Consequently, this article is a demonstration of a general principle rather than an academic proof. In a future article, we will look at the early exercise of American options.

Good luck with your trading, and have a good week!

The strategies presented in this blog are for information and training purposes only, and should not be interpreted as recommendations to buy or sell any security. As always, you should ensure that you are comfortable with the proposed scenarios and ready to assume all the risks before implementing an option strategy.