The Greeks: Delta

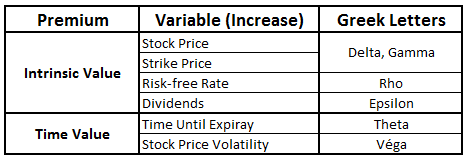
In the last few articles, we have seen that there are several variables that have an impact on the value of options. This table illustrates how an increase in one of the variables affects the values of call and put options.

As you can see, with all other things being equal, when one of the variables moves, we should expect the option premium to change in response. However, knowing that an option’s premium will rise or fall tells us nothing about how much of a change to expect. Variables known as “the Greeks” allow us to anticipate and have a clearer idea of just how much the option’s premium will rise or fall.
The Greeks are variables that measure the sensitivity of an option’s value to a change in the value of one of its underlying valuation variables. The Greeks therefore allow us to measure the risks related to fluctuations in each of these variables.
As you can see, participants in the options market use six Greeks to estimate the impact of a change in market conditions on the values of option positions. Delta and gamma are used to measure the impact on option value of a change in the price of the underlying stock. Rho measures the impact on option value of a change in the interest rate. Epsilon measures the impact on option value of a change in the amount of dividends paid. Theta measures the impact on option value of a change in remaining time. Lastly, vega measures the impact on option value of a change in volatility. Note that rho and epsilon are relatively unimportant to most participants in the options market, given the relative stability of interest rates and the dividends paid during the life of most options. So they will not be discussed further in this series of articles on the Greeks.
The above image illustrates the results associated with the Greeks as generated by the Montréal Exchange’s Options Calculator for CP 20170721 C 200, a call option on the stock of Canadian Pacific Railway Limited (CP). As you can see, the theoretical value of this call is $9.94 and its delta is 0.5143. This tells us that a $1 increase in the price of CP, from $199.55 to $200.55, should cause the value of this call to increase by $0.5143, to $10.4643.
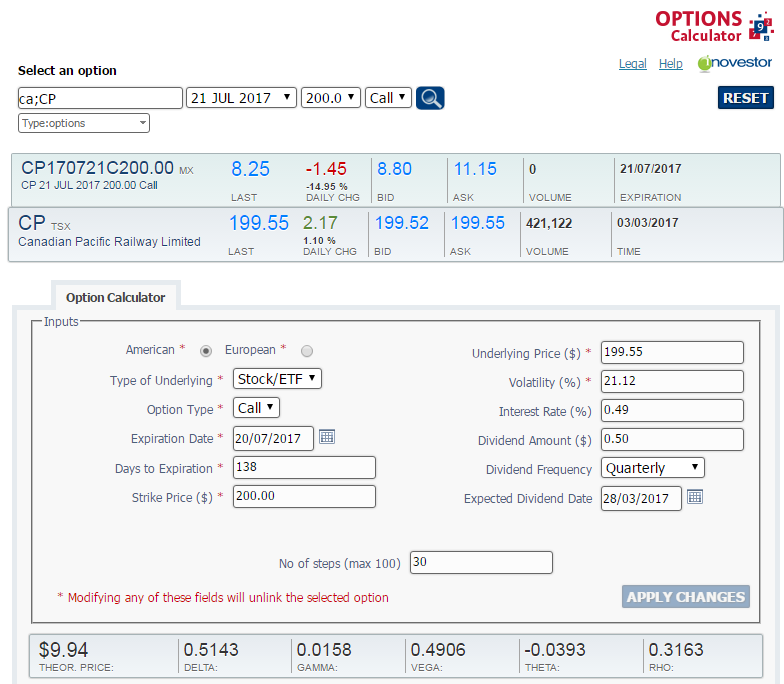
As shown above, by changing the price of CP to $200.55, we effectively obtain a theoretical value of $10.47, confirming our expectations. It is worth remembering that, in this example, the values of all the other variables were held constant. But the result could be different in real life since volatility and remaining time could vary at the same time as the stock price. A subsequent article will take a closer look at this issue.

Now that we know the option’s delta, we can project the potential profit from an options position based on our forecast of the future value of the stock price. This means that we can determine in advance the price that the stock must reach in order to obtain the desired return on our options. But this is not the only use for delta. We can also use it to calculate an equivalent position in shares of the underlying asset. A delta of 0.5143 indicates that a $1 increase in the price of CP will generate a $0.5143 gain on our options. We can therefore infer that holding one call contract CP 20170721 C 200 is equal to holding 51.43 shares, since a $1 increase will produce a gain of $51.43 per options contract (0.5143 x 100 shares per contract). So an investor who would like to have the equivalent of 200 shares of CP in the owned portfolio, but wants to limit risk, should buy four call contracts, CP 20170721 C 200, at $9.94 for a total investment of $3,976, instead of investing the $39,910 it would cost to buy 200 shares of CP at $199.55.
So delta can help us calibrate the number of options contracts to hold in a portfolio in order to hold a desired number of shares of a security we have identified as being of particular interest. This allows us to construct a diversified portfolio that fully reflects our investment objectives, while limiting the funds at risk to the premiums paid on the options.
Good luck with your trading, and have a good week!
The strategies presented in this blog are for information and training purposes only, and should not be interpreted as recommendations to buy or sell any security. As always, you should ensure that you are comfortable with the proposed scenarios and ready to assume all the risks before implementing an option strategy.
President
Monetis Financial Corporation
Martin Noël earned an MBA in Financial Services from UQÀM in 2003. That same year, he was awarded the Fellow of the Institute of Canadian Bankers and a Silver Medal for his remarkable efforts in the Professional Banking Program. Martin began his career in the derivatives field in 1983 as an options market maker for options, on the floor at the Montréal Exchange and for various brokerage firms. He later worked as an options specialist and then went on to become an independent trader. In 1996, Mr. Noël joined the Montréal Exchange as the options market manager, a role that saw him contributing to the development of the Canadian options market. In 2001, he helped found the Montréal Exchange’s Derivatives Institute, where he acted as an educational advisor. Since 2005, Martin has been an instructor at UQÀM, teaching a graduate course on derivatives. Since May 2009, he has dedicated himself full-time to his position as the president of CORPORATION FINANCIÈRE MONÉTIS, a professional trading and financial communications firm. Martin regularly assists with issues related to options at the Montréal Exchange.
The information provided on this website, including financial and economic data, quotes and any analysis or interpretation thereof, is provided solely for information purposes and shall not be construed in any jurisdiction as providing any advice or recommendation with respect to the purchase or sale of any derivative instrument, underlying security or any other financial instrument or as providing legal, accounting, tax, financial or investment advice. Bourse de Montréal Inc. recommends that you consult your own advisors in accordance with your needs before making decision to take into account your particular investment objectives, financial situation and individual needs.
All references on this website to specifications, rules and obligations concerning a product are subject to the rules, policies and procedures of Bourse de Montréal Inc. and its clearinghouse, the Canadian Derivatives Clearing Corporation, which prevail over the content of this website. Although care has been taken in the preparation of the documents published on this website, Bourse de Montréal Inc. and/or its affiliates do not guarantee the accuracy or completeness of the information published on this website and reserve the right to amend or review, at any time and without prior notice, the content of these documents. Neither Bourse de Montréal Inc. nor any of its affiliates, directors, officers, employees or agents shall be liable for any damages, losses or costs incurred as a result of any errors or omissions on this website or of the use of or reliance upon any information appearing on this website.
BAX®, CADC®, CGB®, CGF®, CGZ®, LGB®, MX®, OBX®, OGB®, OIS-MX®, ONX®, SCF®, SXA®, SXB®, SXF®, SXH®, SXM®, SXO®, SXY®, and USX® are registered trademarks of the Bourse. OBW™, OBY™, OBZ™, SXK™, SXJ™, SXU™, SXV™, Montréal Exchange and the Montréal Exchange logo are trademarks of the Bourse. All other trademarks used are the property of their respective owners.
© 2024 Bourse de Montréal Inc. All Rights Reserved.
